Tìm giá trị nhỏ nhất, lớn nhất của biểu thức là một trong những dạng toán lớp 9 được đánh giá là khó, đòi hỏi các bạn học sinh phải vận dụng linh hoạt và khả năng tập trung cao độ khi giải các bài toán biểu thức chứa dấu giá trị tuyệt đối hay dấu căn. Để hiểu rõ hơn, quý bạn đọc hãy tham khảo các thông tin chi tiết có trong bài viết dưới đây.
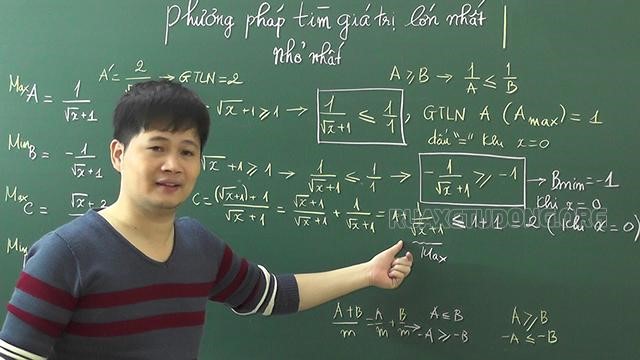
Cách tìm giá trị nhỏ nhất, lớn nhất đã được nhắc tới trong Toán học 7 và được tìm hiểu chi tiết hơn trong Toán học 8, 9. Để dành được điểm 10 toán trong các bài thi học kỳ, thì các bạn học sinh bắt buộc phải nắm chắc kiến thức về tìm giá trị lớn nhất, nhỏ nhất của biểu thức.
Nội dung bài viết
Tìm giá trị nhỏ nhất, lớn nhất của biểu thức đại số

Ước số là gì? Cách tìm ước số của một số và bài tập
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức chứa dấu căn
Có 3 cách đó là:

Cách 1: Biến đổi biểu thức về dạng tổng hoặc hiệu của một số không âm với hằng số
- Khi biến đổi biểu thức thành tổng của một số không âm với hằng số, ta sẽ tìm được giá trị nhỏ nhất của biểu thức đó
- Khi biến đổi biểu thức thành hiệu của một số với số không âm thì ta sẽ tìm được giá trị lớn nhất của biểu thức ấy.
Cách 2: Áp dụng bất đẳng thức Cauchy (Cô -si)
Theo bất đẳng thức Cauchy với 2 số a, b không âm, ta có: a + b ≥
Dấu “=” xảy ra khi và chỉ khi a = b
Cách 3: Áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối
- |a| + |b| ≥ |a+b|. Dấu “=” xảy ra khi và chỉ khi a.b ≥ 0
- |a| – |b|≤ |a +b|. Dấu “=” xảy ra khi và chỉ khi a.b ≤ 0
- Phương pháp giải: Cũng tương tự như cách tìm phương pháp trên, vận dùng tính chất của biểu thức không âm, dấu “=” xảy ra khi A = 0
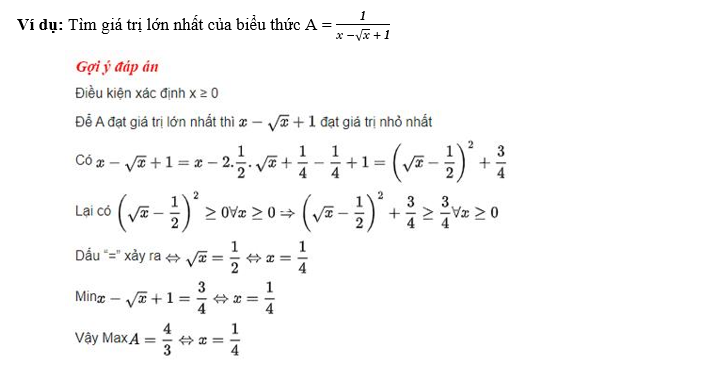
Số nguyên tố là gì? Gồm những số nào? Ví dụ
Tìm giá trị nhỏ nhất, lớn nhất của biểu thức chứa giá trị tuyệt đối
Phương pháp:
- Nếu biểu thức A ≥ m => Giá trị nhỏ nhất của biểu thức A là m
- Nếu biểu thức A ≤ m => Giá trị lớn nhất của biểu thức A là m
Lưu ý:
- Ta có |k.a| ≥ 0 => |x| + a ≥ a; – |k.a| + a ≤ a
- Ta có: |k.x + b| ≥ 0 => |k.x + b| + a ≥ a; -|x +b| + a ≤ a
- Dấu “=” xảy ra ⇔ k.x = 0 hoặc k.x + b = 0
Ví dụ: Tìm giá trị nhỏ nhất của biểu thức B = |x + 2,8| – 7,9
Gợi ý đáp án
|x + 2,8| ≥ 0
=> |x + 2,8| + (-7,9) ≥ 0 + (-7,9)
=> |x + 2,8| – 7,9 ≥ – 7,9
=> B ≥ -7,9
Vậy, giá trị nhỏ nhất (GTNN) của B là – 7, 9
Dấu “=” xảy ra khi x + 2, 8 = 0 => x = – 2, 8
Trung bình cộng là gì? Công thức tính trung bình cộng chính xác 100%
Một số bài tập vận dụng tìm giá trị lớn nhất, nhỏ nhất của biểu thức

Bài tập 1: Tìm giá trị lớn nhất (GTLN) của biểu thức A = 5 – |2x -2|
Gợi ý đáp án:
Ta có: |2x – 2| ≥ 0 ⇔ – |2x – 2| ≤ 0 ⇔ 5 – |2x – 2| ≤ 5
Dấu “=” xảy ra khi |2x – 2| = 0 ⇔ 2x – 2 = 0 => x = 1
Vậy, Amax = 5 khi và chỉ khi x = 1.
Bài tập 2: Tìm giá trị nhỏ nhất của biểu thức: C(x) =
Gợi ý đáp án:
C(x) =
C(x) = +2) – 2x (+2) + ( +2) +2015
C (x) = (+2) ≥ 2015
=> Amin = 2015
Dấu “=” xảy ra khi và chỉ khi x-1=0 => x = 1
Bài tập 3: Tìm giá trị lớn nhất của biểu thức C = 1,5 – |x + 2,1|
Gợi ý đáp án
Ta có: |x + 2,1| ≥ => – | x + 2,1| ≤ 0
=> 1, 5 – |x + 2,1| ≤ 0 + 1, 5
=> C ≤ 1,5
Vậy giá trị lớn nhất của C = 1,5
Dấu “=” xảy ra khi x + 2,1 => x = – 2,1
Hy vọng rằng các nội dung thông tin trên đây về cách tìm giá trị nhỏ nhất ( GTNN) và giá trị lớn nhất (GTLN) của biểu thức sẽ giúp ích bạn. Cập nhật nhiều thông tin hữu ích khác bằng cách truy cập website ruaxetudong.org!
Bài tập 1: Tìm giá trị lớn nhất (GTLN) của biểu thức A = 5 – |2x -2|
Gợi ý đáp án:
Ta có: |2x – 2| ≥ 0 ⇔ – |2x – 2| ≤ 0 ⇔ 5 – |2x – 2| ≤ 5
Dấu “=” xảy ra khi |2x – 2| = 0 ⇔ 2x – 2 = 0 => x = 1
Vậy, Amax = 5 khi và chỉ khi x = 1.
Bài tập 2: Tìm giá trị nhỏ nhất của biểu thức: C(x) =
Gợi ý đáp án:
C(x) =
C(x) = +2) – 2x (+2) + ( +2) +2015
C (x) = (+2) ≥ 2015
=> Amin = 2015
Dấu “=” xảy ra khi và chỉ khi x-1=0 => x = 1
Bài tập 3: Tìm giá trị lớn nhất của biểu thức C = 1,5 – |x + 2,1|
Gợi ý đáp án
Ta có: |x + 2,1| ≥ => – | x + 2,1| ≤ 0
=> 1, 5 – |x + 2,1| ≤ 0 + 1, 5
=> C ≤ 1,5
Vậy giá trị lớn nhất của C = 1,5
Dấu “=” xảy ra khi x + 2,1 => x = – 2,1
Hy vọng rằng các nội dung thông tin trên đây về cách tìm giá trị nhỏ nhất ( GTNN) và giá trị lớn nhất (GTLN) của biểu thức sẽ giúp ích bạn. Cập nhật nhiều thông tin hữu ích khác bằng cách truy cập website ruaxetudong.org!




