Đối xứng trục là một phần kiến thức quan trọng trong Toán học 8 và được tìm hiểu chi tiết trong chương trình Toán học 11. Nếu bạn vẫn chưa nắm chắc được khái niệm, phép đối xứng trục thì đừng bỏ qua các thông tin chi tiết có trong bài viết dưới đây của ruaxetudong.org
Nội dung bài viết
Đối xứng trục là gì? Lý thuyết về đối xứng trục
Hai điểm đối xứng qua một đường thẳng
Hai điểm được gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối 2 điểm đó.
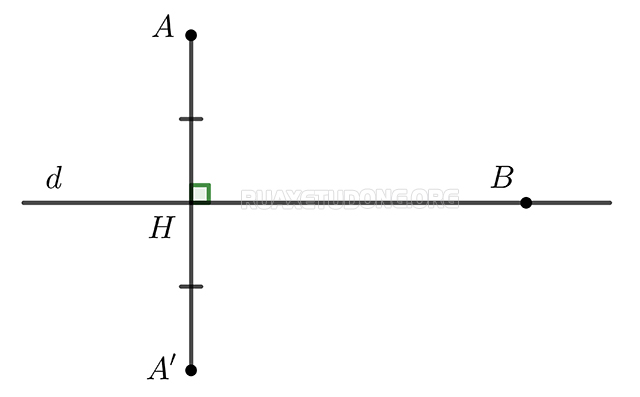
Ví dụ: Hai điểm A, B gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối 2 điểm đó.
=> Quy ước: Nếu điểm B nằm trên đường thẳng d thì điểm đối xứng của B qua đường thẳng d cũng chính là điểm B
Hai hình đối xứng qua đường thẳng
Hai hình được gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một số điểm thuộc hình kia qua đường thẳng d và ngược lại thì đường thẳng d gọi là trục đối xứng của 2 hình đó.
Hình có trục đối xứng
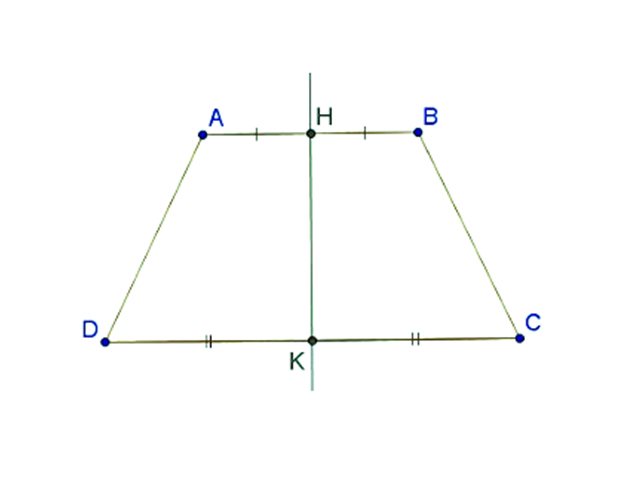
Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H. Ta nói, hình H có trục đối xứng.
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Bài tập đối xứng trục lớp 11
Bài tập 1: Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng:
-
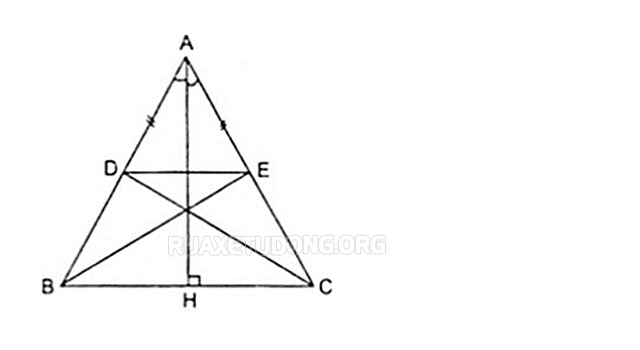
D đối xứng với E qua AH .
- Δ ADC đối xứng với Δ AEB qua AH.
Gợi ý đáp án
- Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
=> D đối xứng với E qua AH.
- Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.
=> B đối xứng với C qua AH, E đối xứng với D qua AH.
Mặt khác, ta có A đối xứng với A qua AH theo quy ước.
=> Δ ADC đối xứng với Δ AEB qua AH.
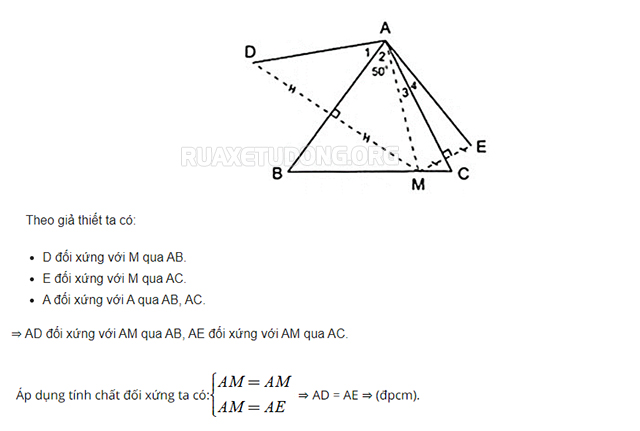
Bài tập 2: Cho Δ ABC có A = 50 , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Chứng minh rằng AD = AE.
Gợi ý đáp án:
Bài tập 3: Cho AB = 6cm, A’ là điểm đối xứng với A qua B, AA’ có độ dài bằng bao nhiêu?
Gợi ý đáp án:
Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Khi đó, A’ là điểm đối xứng với A qua B thì AB = BA’ = 6cm
=> AA’ = AB + BA’ = 6 + 6 = 12cm
Đồng quy là gì? Tìm hiểu về đồng quy, đường thẳng đồng quy trong toán học
Phép đối xứng trục là gì? Tính chất phép đối xứng trục
Định nghĩa phép đối xứng là gì?
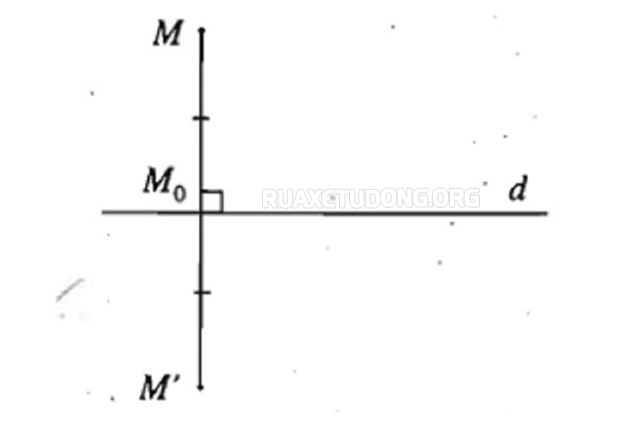
Phép đối xứng được định nghĩa như sau: Phép biến hình cho phép biến mỗi điểm M thuộc đường thẳng d thành chính nó, cho phép biến mỗi điểm M không thuộc đường thẳng d thành điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’. Đó được gọi là phép đối xứng trục d hay phép đối xứng qua đường thẳng d.
Tính chất của phép đối xứng trục
Tính chất 1: Phép đối xứng qua đường thẳng bảo toàn khoảng cách giữa 2 điểm bất kỳ. Nghĩa là thông qua trục đối xứng, điểm M và M’ sẽ có khoảng cách bằng nhau hoặc hình A sẽ giống hình A’ từ kích thước, hình dáng đến chu vi, diện tích.
Tính chất 2: Phép đối xứng qua đường thẳng giúp:
- Biến đường thẳng thành đường thẳng
- Biến đoạn thẳng thành đoạn thẳng bằng nó
- Biến tam giác thành tam giác bằng nó
- Biến đường tròn thành đường tròn có cùng bán kính
- Biến một tia thành tia
- Biến một góc thành góc
Nói cách khác, nó sẽ biến các hình dáng hình học thành một tia, đường thẳng, hình học y hệt mà không làm biến dạng bất kỳ hình học nào.
Số hữu tỉ là gì? Số vô tỉ là gì? Phân biệt số hữu tỉ và số vô tỉ
Các dạng bài tập phép đối xứng trục
Xác định ảnh của một hình: Với những bài toán như thế này, phương pháp giải chính đó là sử dụng phép đối qua đường thẳng hoặc dùng biểu thức tọa độ biểu thức tọa độ của phép đối qua đường thẳng mà trục đối xứng là các trục tọa độ Ox, Oy. Ngoài ra, bạn cũng có thể dùng biểu thức vectơ.
Các bài tập toán dựng hình: Ngoài bài tập về xác định, tìm ảnh của đường thẳng qua phép đối xứng trục thì có một dạng toán khác có thể sử dụng phép biến hình để giải là bài toán dựng hình. Với bài toán dựng hình, cần phải xác định nó là hình ảnh của một điểm đã biết qua phép đối xứng đường thẳng hoặc có thể xem M là giao điểm của một đường cố định và một ảnh của đường đã biết qua phép đối xứng.
Hy vọng rằng, các thông tin có trong bài viết “Đối xứng trục là gì? Phép đối xứng trục là gì? Bài tập ví dụ” hy vọng sẽ giúp ích với bạn. Truy cập ruaxetudong.org để cập nhật thêm nhiều thông tin hữu ích khác về toán học.




