Lũy thừa là kiến thức có trong chương trình Toán lớp 6. Đây là kiến thức quan trọng, được ứng dụng nhiều trong toán học và thực tiễn. Trong bài viết này, ruaxetudong.org sẽ cập nhật các thông tin chi tiết về khái niệm, công thức tính và ví dụ, chắc chắn sẽ giúp ích với bạn rất nhiều đó!
Nội dung bài viết
Lũy thừa là gì?
Lũy thừa là phép toán hai ngôi của toán học, thực hiện trên hai số a và b, kết quả của phép toán lũy thừa là tích số của phép nhân có b thừa số a nhân với nhau. Lũy thừa ký hiệu là a, đọc là lũy thừa bậc b của a hay a mũ b, số a gọi là cơ số, b gọi là số mũ.
Phép toán ngược với phép tính lũy thừa là phép khai căn. Lũy thừa có nghĩa là “nhân chồng chất lên”.
Các dạng lũy thừa của biểu thức
Lũy thừa được chia làm 3 dạng, đó là:
Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương. Với a là một số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a. Định nghĩa lũy thừa với số mũ nguyên cũng giống như định nghĩa chung về lũy thừa.
Công thức tổng quát như sau:
= a.a.a.a.a…..a (n là thừa số của a)
Với 
thì = 1. 
Lưu ý:
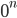và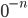 
không có nghĩa- Lũy thừa với số mũ nguyên có các tính cách tương tự của lũy thừa với số mũ nguyên dương.
Lũy thừa với số mũ hữu tỉ
Cho số thực a dương và số hữu tỉ r = 
, trong đó m ∈ Z, n ∈ N, n>=2
Lũy thừa của số a với số mũ r là số 
xác định bởi 
Đặc biệt, khi m = 1 : 
Lũy thừa với số mũ thực
Cho a>0, a ∈ R, là một số vô tỉ, khi đó 
với 
là dãy số hữu tỉ thỏa mãn 
Vận tốc là gì, công thức tính vận tốc, quãng đường và thời gian
Tính chất lũy thừa với số mũ tự nhiên
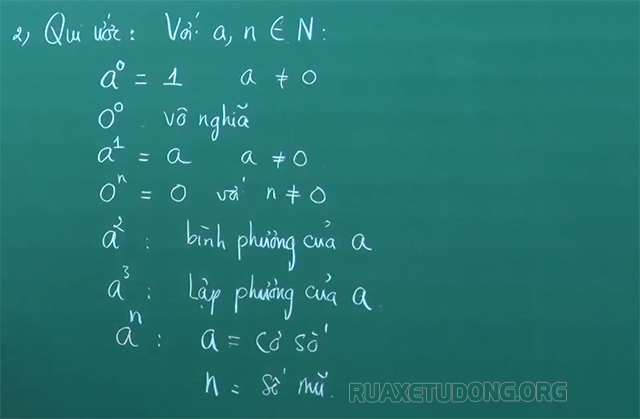
- Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
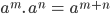
- Khi chia hai lũy thừa cùng cơ số, ta giữ nguyên số và trừ các số mũ:
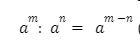(a khác 0, m>=n) - Mở rộng
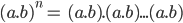gồm n thừa số a.b =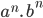 
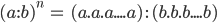gồm n thừa số a, n thừa số b = 
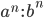(b khác 0)
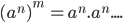(gồm m thừ số ) =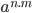 
Các công thức lũy thừa
Các công thức lũy thừa đã được đề cập tới trong SGK Toán lớp 6. Có các công thức tính lũy thừa như sau:
Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau. Công thức tính như sau: 
( a≠ 0, m ≥ 0)
Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ với nhau.
Công thức như sau: 
Lũy thừa của lũy thừa
Công thức như sau: 
Ví dụ: 
Nhân hai lũy thừa cùng cơ mũ, khác cơ số
Công thức như sau: 
Ví dụ: 
Chia hai lũy thừa cùng số mũ, khác cơ số
Công thức như sau: 
Ví dụ: 
Trung bình cộng là gì? Công thức tính trung bình cộng chính xác 100%
Các dạng bài tập về lũy thừa với số mũ tự nhiên
Dạng 1: Viết kết quả phép tính nhân, chia dưới dạng lũy thừa
Phương pháp giải: Để viết kết quả phép tính dưới dạng lũy thừa ta biến đổi phép tính về dạng phép nhân các lũy thừa cùng cơ số hoặc phép chia hai lũy thừa cùng cơ số, rồi áp dụng quy tắc nhân lũy thừa cùng cơ số hoặc chia hai lũy thừa cùng cơ số để viết gọn kết quả.
Ví dụ: Viết gọn các tích sau thành lũy thừa
- 3.3.3.3.7.7.7.7
- 1000. 10000. 100000
Lời giải:
= 
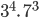
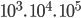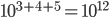
Dạng 2: So sánh các số viết dưới dạng lũy thừa, tìm số mũ của lũy thừa
Để so sánh các số viết dưới dạng lũy thừa, ta có thể thực hiện 3 cách sau:
Cách 1: Đưa lũy thừa về cùng cơ số là số tự nhiên rồi so sánh hai số mũ. Nếu m > n thì 
Cách 2: Đưa lũy thừa về cùng số mũ rồi so sánh hai cơ cố. Nếu a > b thì 
Cách 3: Tính cụ thể từng lũy thừa rồi so sánh
Dạng 3: Tìm chữ số tận cùng của một số dạng lũy thừa
Dựa vào các tính chất dưới đây để tìm số tận cùng của dãy số lũy thừa:
- Một số chính phương (là bình phương của số tự nhiên) có tận cùng là 0, 1 , 4, 5, 6 ,9.
- Một số nguyên tố lớn hơn 5 chỉ có thể tận cùng là 1, 3, 7, 9
- Chữ số tận cùng của 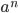chính là chữ số tận cùng của
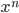(với x là chữ số tận cùng của a) - Các số có chữ số tận cùng là 0, 1, 5, 6 khi nâng lên lũy thừa bất kỳ thì chữ số tận cùng không thay đổi.
- Các chữ số có chữ số tận cùng là 4, 9 khi nâng lên lũy thừa bậc lẻ thì chữ số tận cùng vẫn thay đổi.
- Các số có tận cùng chữ số là 3, 7, 9 khi nâng lũy thừa bậc 4n (n là số tự nhiên) thì chữ số tận cùng là 1.
- Các số có chữ số tận cùng là 2, 4, 8 khi nâng lũy thừa bậc 4n (n là số tự nhiên) thì chữ số tận cùng là 6
- Một số tự nhiên khi nâng lên lũy thừa bậc 4n +1 (n là số tự nhiên) thì chữ số tận cùng sẽ không thay đổi.
- Số tự nhiên có chữ số tận cùng là 3 thì khi nâng lên lũy thừa bậc 4n +3 sẽ có chữ số tận cùng là 7, số tự nhiên có chữ số tận cùng là 7 khi nâng lên lũy thừa bậc 4n+3 sẽ có chữ số tận cùng là 3.
- Số tự nhiên có chữ số tận cùng là 2 thì khi nâng lên lũy thừa 4n+3 thì chữ số tận cùng là 8, số tự nhiên có chữ số tận cùng là 8 khi nâng lên lũy thừa bậc 4n + 3 sẽ có chữ số tận cùng là 2.
- Các số tự nhiên có chữ số tận cùng là 0,1, 4, 5, 6, 9 khi nâng lên lũy thừa bậc 4n + 3 sẽ không thay đổi chữ số tận cùng.
- Chữ số tận cùng của một tổng các lũy thừa được xác định bằng cách tính tổng các chữ số tận cùng của từng lũy thừa trong tổng.
Ví dụ 1: Tìm chữ số tận cùng của 7^99
Lời giải: Ta có 99 = 4n + 1 (n thuộc N) do đó 7^99 có tận cùng là 7
Ví dụ 2: Tìm chữ số tận cùng của tổng A = 2^1 + 3^5 + 4^9 + … + 2004^8009
Lời giải
Mọi lũy thừa trong tổng A đều có số mũ ở dạng 4n + 1 với n = 0, 1, 2, …., 2002. Do đó mọi lũy thừa trong tổng A và các cơ số tương ứng đều có cùng chữ số tận cùng.
Ta có: (2 + 3 + 4 + … + 9) + 199.(1 + 2 + 3 + …. + 9) + (1 + 2 + 3 + 4) = 200.(1 + 2 + 3 + … + 9) + (2 + 3 + 4) = 9009.
Trọng lượng là gì? Khối lượng là gì? – Công thức tính, đơn vị đo
So sánh hai lũy thừa cùng số mũ
Nếu hai lũy thừa có cùng số mũ (lớn hơn 0) thì lũy thừa nào có cơ số lớn hơn thì sẽ lớn hơn: 
Ví dụ: So sánh 4^5 và 6^5
Ta thấy, 2 số trên có cùng số mũ là 5 và 4 < 6 => 
Ngoài ra, để so sánh 2 lũy thừa ta dùng tính chất bắc cầu – tính chất đơn giản của phép nhân. a < b thì ac < bc (c > 0)
Ví dụ: So sánh 
và 
Ta thấy các cơ số 32 và 16 khác nhau nhưng đều là luỹ thừa của 2 lên ta tìm cách đưa và về lũy thừa cùng cơ số 2.
= 
= 
= 
= 
Vì 
< 
=> 
< 
Sử dụng máy tính cầm tay để tính lũy thừa
Tuy sách giáo khoa không trình bày cách tính căn và lũy thừa của một số nhưng trong thực tế các học sinh đều sử dụng một trong các loại máy CASIO fx-500 hoặc fx-570 (MS hoặc ES/ ES Plus). Dưới đây là giới thiệu vắn tắt về cách tính lũy thừa bằng máy tính cầm tay mà bạn có thể áp dụng.
Vào mode tính toán bằng cách ấn các phím MODE 1. Sau đó nhập số cần lấy căn kết thúc nhấn phím = sẽ được kết quả. Với căn bậc hai và căn bậc ba thì không cần nhập chỉ số căn, với các căn bậc bốn trở lên thì bạn cần nhập chỉ số căn (các máy CASIO fx-500 MS và CASIO fx-570 MS, Casio fx-580VN X, nhập chỉ số căn ấn các phím SHIFT, x√x máy CASIO fx-570MS ấn phím SHIFT, □√◻ nhập chỉ số ▹▹, sau đó nhập số cần lấy căn và ấn phím = để được kết quả.
Với các nội dung thông tin trên đây về lũy thừa, hy vọng sẽ giúp ích với bạn. Cập nhật thêm nhiều thông tin hữu ích khác về toán học bằng cách truy cập website ruaxetudong.org.
