Khoảng cách giữa 2 đường thẳng chéo nhau là chương trình Toán học quan trọng được đề cập trong chương trình lớp 11. Các câu hỏi về tính khoảng cách giữa 2 đường thẳng xuất hiện rất nhiều trong các bài thi THPT Quốc gia vậy nên các bạn học sinh cần phải đặc biệt chú ý khi ôn luyện. Để nắm chắc kiến thức quan trọng này, quý bạn đọc đừng bỏ qua nội dung dưới đây của ruaxetudong.org
Định nghĩa khoảng cách giữa 2 đường thẳng chéo nhau
Trong không gian tọa độ Oxyz, có 4 vị trí tương đối của 2 đường thẳng đó là trùng nhau, cắt nhau, chéo nhau và song song. Trường hợp 2 đường thẳng chéo nhau thì khoảng cách giữa chúng chính là độ dài đoạn vuông góc chung của 2 đường thẳng. Trong đó, đoạn thẳng nối 2 điểm trên 2 đường thẳng chéo nhau, đồng thời vuông góc với 2 đường thẳng đó là đoạn vuông góc chung.
Hiểu đơn giản, khoảng cách giữa 2 đường thẳng chéo nhau là độ dài đoạn vuông góc chung của 2 đường thẳng đó.
Kí hiệu: d (a,b) = MN trong đó M![]() a, N
a, N![]() b và MN
b và MN ![]() a, MN
a, MN ![]() b
b
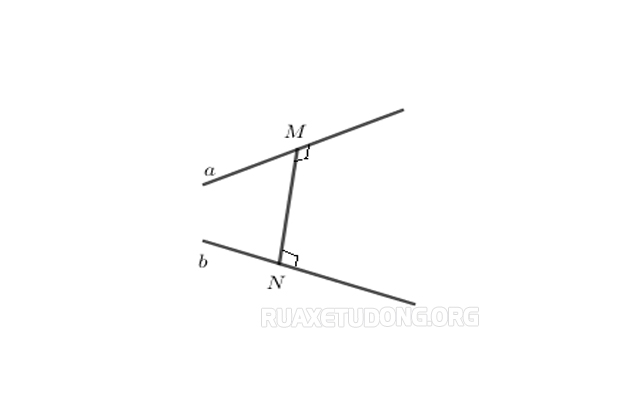
Khoảng cách giữa 2 đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó chưa đường thẳng còn lại.
Khoảng cách giữa 2 đường thẳng chéo nhau sẽ bằng khoảng cách giữa 2 mặt phẳng song song lần lượt chứa 2 đường thẳng đó.
Kí hiệu: d (a,b) = d (a,(Q)) = d (b,(P)) = d ((P),(Q)). Trong đó, (P) và (Q) là hai mặt phẳng lần lượt chứa các đường thẳng a, b và (P) // (Q). Và được minh họa bằng hình vẽ sau:
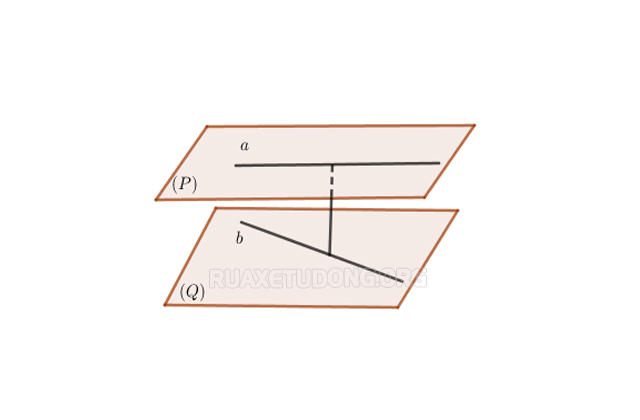
Tính khoảng cách giữa 2 đường thẳng chéo nhau
Để tính khoảng cách giữa 2 đường thẳng chéo nhau bạn có thể áp dụng một trong 4 phương pháp dưới đây mà ruaxetudong.org đã tổng hợp. Cụ thể:
Phương pháp 1: Dựng đoạn vuông góc chung MN của a và b, khi đó d (a,b) = MN
Khi dựng đoạn vuông góc chung MN, có thể sẽ gặp phải 2 trường hợp sau:
Trường hợp 1: ∆ và ∆’ vừa chéo vừa vuông góc với nhau
Khi gặp trường hợp này, ta sẽ:
- Chọn mặt phẳng (α) chứa ∆’ và vuông góc với ∆ tại I
- Trong mặt phẳng (α) kẻ đường thẳng IJ vuông góc với ∆’
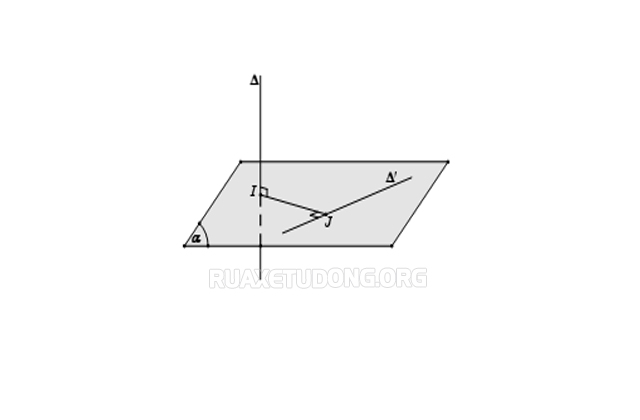
=> IJ là đoạn vuông góc chung và d (∆, ∆’) = IJ.
Trường hợp 2: ∆ và ∆’ chéo nhau mà không vuông góc với nhau
- Chọn một mặt phẳng (α) chứa ∆’ và song song với ∆
- Dựng d là hình chiếu vuông góc của ∆ xuống (α) bằng cách lấy điểm M thuộc ∆ dựng đoạn MN vuông góc với (α) . Khi đó, d là đường thẳng đi qua N và song song với ∆
- Gọi H là giao điểm của đường thẳng d với ∆’, dựng HK // MN
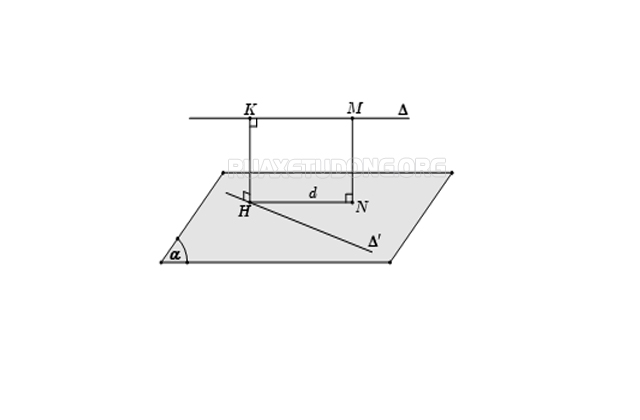
=> HK là đoạn vuông góc chung và d (∆, ∆’) = HK = MN.
Hoặc:
- Chọn mặt phẳng (α) vuông góc với ∆ tại I
- Tìm hình chiếu d của ∆’ xuống mặt phẳng (α)
- Trong mặt phẳng (α), dựng IJ vuông góc với d, từ J dựng đường thẳng song song với ∆ và cắt ∆’ tại H, từ H dựng HM // IJ
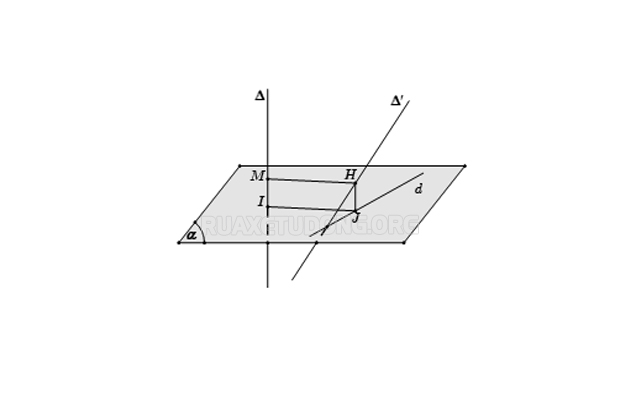
=> HM chính là đoạn vuông góc chung và d (∆, ∆’) = HM = IJ.
Phương pháp 2: Chọn mặt phẳng (α) chứa đường thẳng ∆ và song song với ∆’. Khi đó, d (∆, ∆’) = d (∆’, (α)).
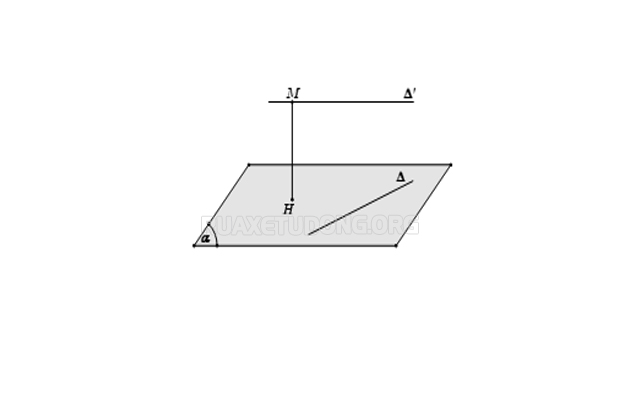
Phương pháp 3: Dựng 2 mặt phẳng song song và lần lượt chứa 2 đường thẳng. Khoảng cách giữa 2 mặt phẳng đó chính là khoảng cách giữa 2 đường thẳng cần tìm.
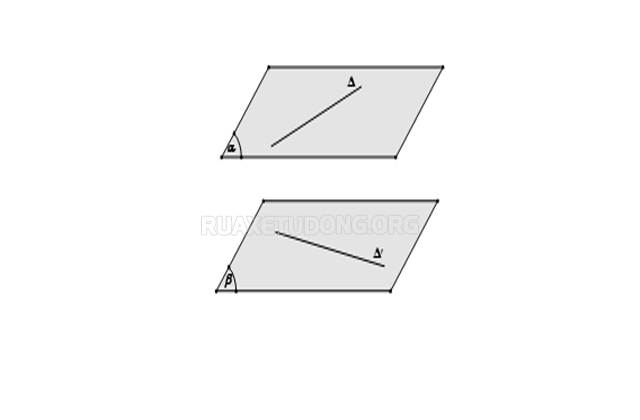
Phương pháp 4: Sử dụng phương pháp vec tơ

Với các thông tin có trong bài viết, hy vọng sẽ giúp bạn nắm chắc được thông tin về khoảng cách giữa 2 đường thẳng chéo nhau. Để có thêm nhiều thông tin khác về Toán học, quý bạn đọc hãy truy cập website ruaxetudong.org, chắc chắn sẽ giúp ích bạn rất nhiều đó.
R là tập số gì? R là gì trong toán học? Cho ví dụ
Vận tốc là gì, công thức tính vận tốc, quãng đường và thời gian




